ECDSA son las siglas en inglés de Elliptic Curve Digital Signature Algorithm (Algoritmo de Firma Digital de Curva Elíptica). Este sistema, se utiliza para crear una firma digital que permite la verificación por parte de terceros sin comprometer la seguridad.
Principios básicos de ECDSA
El funcionamiento matemático y algorítmico de ECDSA es bastante complejo. Para empezar, ECDSA basa su funcionamiento en base a una ecuación matemática que dibuja una curva. El proceso, a grandes rasgos, sería el siguiente:
Pulsa aquí para abrir de forma GRATUITA y segura tu cuenta de usuario en español y recibe un regalo de 15€.
El algoritmo ECDSA funciona mediante un mecanismo de criptografía llamado, criptografía asimétrica. Este sistema de firmado, genera dos claves que reciben el nombre de clave privada y clave pública. Ambas claves están relacionadas por una compleja operación matemática realizada sobre una función de curva elíptica.
Bajo este esquema de funcionamiento, ECDSA garantiza en primera instancia lo siguiente:
- Firmas únicas e irrepetibles para cada conjunto de generación de claves privadas y públicas.
- La imposibilidad práctica de falsificar las firmas digitales. Esto es así porque la potencia computacional necesaria para ello, está fuera de los límites actuales.
Gracias a estas dos características, ECDSA se considera un estándar seguro para desplegar sistemas de firmas digitales. Su uso en la actualidad es tan variado, que hay aplicación de las mismas en casi todos los campos informáticos. Por ejemplo, la infraestructura de certificados de seguridad SSL y TLS de Internet hace uso intensivo de ECDSA. El Bitcoin, precursor de la tecnología blockchain, también hace uso de ECDSA para alcanzar el elevado nivel de seguridad que lo caracteriza.
Sobre esa curva, se elige un punto al azar y se considera que es su punto de origen.
Seguidamente, se genera un número aleatorio, es precisamente este número aleatorio, el que conoceremos como la clave privada.
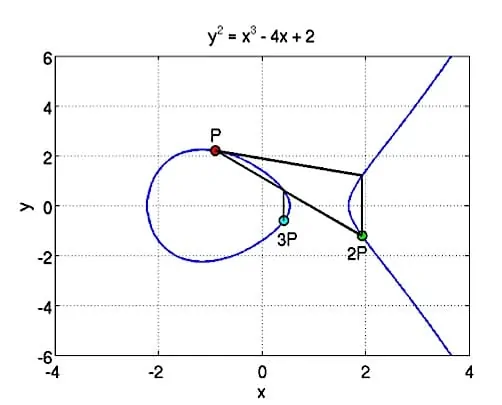
Luego, haciendo uso la clave privada y el punto de origen, realizas otra ecuación y obtenemos un segundo punto en la curva, esa es tu clave pública. Es precisamente, uso de esa nueva ecuación junto al punto de origen y la clave pública, la que permite establecer la relación entre la clave pública y la privada.
Este proceso es considerado seguro, porque de momento solo puede hacerse en un sentido. Es decir, solo es posible establecer la relación matemática desde clave privada a pública, pero al contrario no.
De esta forma, cuando un usuario quiera firmar un archivo, usará su clave privada (el número aleatorio) con un hash del archivo (un número único para representar el archivo) en una ecuación mágica y eso le dará su firma. Si alguien quiere comprobar la veracidad de la información, solo necesita la clave pública y con ella será capaz de verificar la autenticidad.
Así pues, las claves públicas pueden ser conocidas por todos, sin poner en riesgo la autenticidad de nuestra firma, pues la clave pública solo sirve para verificar, no para firmar.
¿Por qué usamos ECDSA?
La necesidad de crear un sistema de firmas como el de ECDSA nace de poder compartir datos de forma segura. En un mundo conectado por redes, se hace necesario un esquema en el que podamos compartir información y validarla. Todo ello sin necesidad de revelar secretos. Veámoslo con el siguiente ejemplo:
Una compañía ha realizado un informe económico sobre sus actividades. Este informe es entregado a ciertos inversores con limitado nivel de acceso a información. Estos inversores desean verificar la autenticidad del informe y los datos ofrecidos.
En este punto nos preguntamos: ¿El administrador le dará la clave de acceso total a los datos de la empresa?. O por el contrario, ¿No le dará acceso a la información a los inversores para que puedan verificarla?
Ambas situaciones no son buenas y el uso de ECDSA puede solucionarla gracias a un tercer enfoque:
El administrador hace uso de un sistema de firmas asimétricas ECDSA. Con ello, el administrador firma el informe con su clave privada, y da la clave pública a los inversores. Inmediatamente después, los inversores pueden verificar usando la clave pública, la autenticidad de la información ofrecida. Esto sin la necesidad de tener acceso irrestricto a los datos.
Clave privada, pública y firmas
El esquema de funcionamiento de ECDSA se basa en los siguientes tres pilares:
- La clave privada, que en realidad es un número secreto conocido solo por la persona que lo generó. Una clave privada es esencialmente un número generado aleatoriamente. En Bitcoin, alguien con la clave privada que corresponde a los fondos en la blockchain es el único que puede gastar esos fondos.
- La clave pública, el cual es un número generado a partir de una relación matemática usando la clave privada. Solo se puede obtener conociendo la clave privada con anterioridad, y no al revés. Esta clave se genera con el fin de compartirse públicamente para que otros puedan determinar si una firma es genuina.
La firma en realidad, es un simplemente un número que indica al verificador que se realizó la operación de firma digital, de forma exitosa. Una firma se genera matemáticamente a partir de el hash de lo que se firmará, más una clave privada. La firma en sí es dos números conocidos como «r» y «s«. Con la clave pública, se puede usar un algoritmo matemático en la firma. La finalidad de esto es determinar que se produjo originalmente a partir del hash y la clave privada. Un sistema que funciona perfectamente, sin necesidad de conocer la clave privada.
ECDSA y la tecnología blockchain
Uno de los principales problemas a los que se enfrentó Satoshi Nakamoto con el Bitcoin, fue la distribución de las claves públicas. La visión de Nakamoto era la de permitir compartir claves públicas de poca extensión, seguras, con bajo coste computacional y sencillas de usar.
Estas características serían alcanzables gracias a la criptografía de curva elíptica. Por lo tanto, está es la razón por la que Nakamoto decidió usar ECDSA para su sistema. Y con ello, se aseguraba que:
- Fuese un sistema muy seguro. Satoshi decidió usar el estándar de curva elíptica secp256k1 para el Bitcoin. Esta curva elíptica tiene una seguridad muy bien probada, por lo que resultó perfecta para aplicarla.
- El coste computacional de generar claves y validar firmas es muy bajo.
- Permite la generación de claves públicas infinitas.
Sin embargo, las claves ECDSA de 256 bits son muy extensas. Teniendo en cuenta en eso, Nakamoto decidió refactorizar las claves públicas para hacerlas más cortas. Fue así que usando codificación Base58 y funciones hash como SHA-256 y RIPEMD-160, redujo el tamaño de las claves públicas y creó las direcciones Bitcoin.
Por ejemplo esta dirección: 1PfS6w6MonCT976xe2jD9tqwo8QkDnonRW.
Todo ello resultó, es un sistema computacional que permitía a sus usuarios enviar y recibir bitcoin de forma segura.
Jugando con ECDSA
En Internet existen muchos espacios donde podemos jugar y conocer un poco más sobre cómo funciona ECDSA. Uno de esos sitios es el Github de Kenji Urushima.
Urushima es un trabajador de Fuji Xerox en Japón. En su página web tiene una herramienta interactiva que ayuda a entender como funciona ECDSA. En este sitio, podremos crear las claves privadas y públicas y firmas mensajes personalizados. Experimentar un poco puede resultar clave para comprender algo más cómo funciona este sistema de firmado digital.
Pulsa aquí para abrir de forma GRATUITA y segura tu cuenta de usuario en español y recibe un regalo de 15€.

 Autor
Autor